https://github.com/QInzhengk/Math-Model-and-Machine-Learning @TOC
题目及摘要
关键词：数据清洗 线性插值 线性最小二乘拟合 多元回归分析 时间序列预测
一、任务重述 1
二、任务的分析 2
任务一的分析:任务一是一个关于数据处理的问题，要求我们对于给定原始数据，识别异常、冗余或丢失等问题数据，并完成对问题数据的修正及缺失数据的填补。对此，首先观察所给出的原始数据，发现在时间存在大量的缺失值。其次，还可能存在着冗余、异常或丢失数据。通过对原始数据的特征分析，清洗数据，对冗余值进行处理，利用标准差法和箱线图法对异常数据进行修正，接着，利用线性插值对缺失值进行填补。 任务二的分析：任务二可以分解成两部分，第一部分是求解两个变量间的关系，第二部分是求解多变量之间的关系，并对data 2中的缺失值进行填补。第一部分的自变量为时间，因变量为流量、速度和时间占有率三个参数。对于大样本的数据，通常采用线性拟合的办法，获得一个最佳拟合函数，表达出因变量随自变量的变化规律。第二部分的因变量可以为时间占有率，那么自变量即是流量和速度。探索三个变量之间的关系可以使用多元回归分析，得到三个变量的回归系数，进一步得到三个变量间的数学模型。最后，利用得到的数学模型对给定数据样本中的缺失值进行填补。 任务三的分析：任务三要求我们根据交通系统的特点建立适用、合理的预测模型，并将data 3中缺失的速度、流量和时间占有率的数据进行补充。首先，对于基于时间按照先后顺序排列的某大样本的某种统计指标的预测问题，常用的方法有神经网络预测方法和时间序列预测等方法。其中，时间序列预测模型包括平稳时间序列模型和非平稳时间序列模型。在任务二中，探讨了交通系统在时间维度上具有较强的依赖性和周期性，因此，可以合理的假设，交通系统在更短的时间内也可能具备一定的周期性。因此，针对于本题，考虑使用非平稳时间序列预测。
三、模型假设 3
（1）数据样本中不存在不精确数据； （2）该路段可能有交通事故，或车辆超速行驶等情况的发生； （3）该地区，公路的最高车速限制为60 km⋅h^-1； （4）该地区城市道路和公路的设计通行能力为1000-4000 veh⋅h-^1；
四、符号说明 3
| 符号 | 含义 |
|---|---|
| vbef | 代表原始数据中的速度 |
| qbef | 代表原始数据中的流量 |
| v | 代表速度 |
| q | 代表流量 |
| O | 代表占用率 |
| outlier | 回归系数 |
| R | 复相关系数 |
| d | 差分次数 |
| p | 代自由回归项数 |
| q | 滑动平均项数 |
五、模型的建立与求解 3
5.1 任务一：数据清洗与缺失值填补 3
5.1.1求解思路 3
任务一要求将一个给定的交通数据样本中存在的问题数据进行修正，并对缺失值进行填补。问题数据样本一般主要包含三种“脏数据”，分别是丢失数据、冗余数据和异常数据。首先，在统一时间步长的基础上，要建立问题数据的判别规则，分别筛选出样本中的丢失数据，冗余数据和异常数据，并相应地对其进行补齐、约简和替换，保留正确数据。接着，利用缺失值填补模型，将清洗后的数据进行缺失值填补。最终，得到具有完整数据的数据样本。解题思路示意图如下图1.1所示。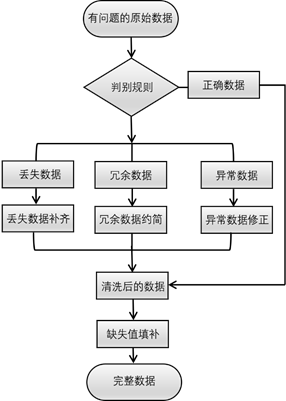 
图1.1 数据预处理流程图
5.1.2数据清洗 4
5.1.2.1冗余数据与丢失数据清洗模型的建立与求解 数据几乎没有完美的，大多数数据都存在着质量问题，因此，数据质量分析是数据分析中的至关重要的一步，是之后进行一切探索的基础。[1]对于实际生活中交通监测，在ITS数据收集过程中，由于信号不稳定及路面状况复杂等原因，得到的数据经常出现异常、丢失、冗余等问题。比如，在较少车流量的情况下，占用率却偏高，这种不符合实际情况以及不复合期望范围内的现象，便是数据异常；其次，它也违反了交通流理论。而当车辆密度过大，或者交通检测器扫描不稳定，信号传输、存储设备出现故障等情况发生时，则经常导致数据的丢失。数据冗余是指，当某段监测路段或交叉路口布置的交通检测器密度过高，导致对同一单位的重复监测，从而引起的某时间点集合中的数据具有高相似性的现象。当这些“脏数据”包含在提供到交通调控应用的数据时，必定会引起巨大的安全隐患。因此，在利用原始数据进行分析处理时，必须要先清洗数据，即，补齐丢失数据，修正异常或冗余的数据。[2] 首先，观察原始数据，根据每5 min取值，取时时长从1月1日00:00到1月31日00:00，共30天，因此，理论上应共有302460/5=8640组数据，而监测到仅有8636组数据，由此可见，样本丢失了4组数据。将一段时间内收集得到数据划分为一个时间段，例如，将08:00:00到08:05:00中得到数据都定义为08：00这一时段的数据，利用python对给定数据中所有时间段进行扫描，检索是否有数据丢失，如有丢失，则进行均值填补。扫描结果得出，data 1中存在4组丢失数据，分别为：1月9日0:10，1月13日10:40，1月26日13:40和1月26日13:45。 接着，对原始数据进行值分析，这有利于在总体上展示数据的自然分布情况，例如，数据的唯一值、变量中的空值等。此模型中，具体统计信息如表1.1所示。
表格 1.1 数据统计描述
| 数值名称 | 速度（v） | 流量（q） | 占用率(O) |
|---|---|---|---|
| 总记录数 | 8640 | 8640 | 8640 |
| 非空值数 | 5981 | 6045 | 6045 |
| 空值占比 | 30.77% | 30.03% | 30.03% |
| 平均值 | 65.89 | 63.68 | 10.32 |
| 标准差 | 29.96 | 39.03 | 10.00 |
| 最小值 | 3.55 | 0 | 0 |
| 下四分位数 | 52.70 | 30.00 | 3.50 |
| 中值 | 57.61 | 64.00 | 8.24 |
| 上四分位数 | 60.74 | 91.00 | 12.60 |
| 最大值 | 142.74 | 182.15 | 107.65 |
由上表可以发现，三个参数的空值占比均为30%左右，处于5%~85%范围内，说明缺失值占据了总记录数的较大比例，如果使用删除法会导致样本量减少，削弱统计功效。因此，应当选择替换法对缺失值进行填补。此外，原始数据中可能存在着冗余数据，冗余数据的存在会影响数据分析和挖掘结果的准确性。因此，接下来对数据进行重复观测处理，在Pandas中使用duplicated方法，返回数据行每一行的检验结果，即每一行返回一个bool值，使用drop. Duplicates方法移除重复值。结果显示，给定的原始数据中不存在冗余数据。因此，接下来对原始数据进行清洗。
5.1.2.2异常数据清洗模型的建立与求解
1. 箱线图法
关于异常值的检测与处理，箱线图是一种很常用的方法。箱线图是指主要利用一组数据的上、下边缘，中位数和上、下四分位数来展示一组数据的离群信息以及数据是否对称等信息的一种统计方法。应当注意，离群数据不一定都是异常数据。这里，箱线图法的判别公式以及判别过程如图1.2所示，其中，Q1为下四分数（25%），Q3为上四分数（75%），IQR为上四分位数与下四分位数的差。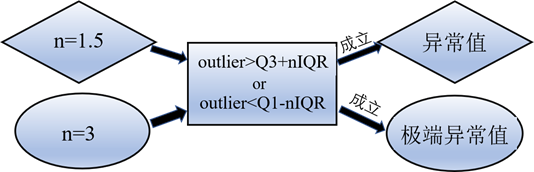
图1.2 箱线图判别流程图 由上箱线图法，结合python，对给定的原始数据进行扫描，得到结果发现速度、流量和占用率的给定原始数据都存在异常值。速度、流量和占用率的直方图和核密度图如图1.3所示，图中的直方图和核密度曲线显示，数据分布形状是有偏的。 
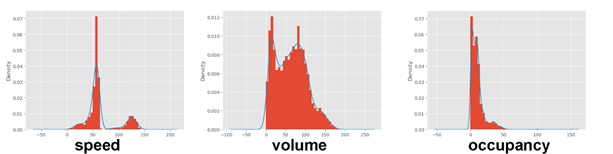图1.3 直方图和核密度曲线 最后，给出异常值处理前后的统计描述对比，如表1.2所示。根据箱线图法得到速度、容量和占用率的上限临界值分别为72.80，182.5和26.25，说明此模型对异常数据的修正标定了一个合理的上限。此外，可以发现异常值的替换，不仅改变了给定的原始数据的均值，标准差和最大值，并且这些值改变后都降低了，说明此箱线图法对异常值的修正具有效果的良好。例如，给定原始数据中的最大占用率为107.65%，这明显不符合实际情况，属于异常数据。经替换后，现占用率为26.17%，符合客观事实。 表1.2 异常值处理前后的统计描述对比 count mean std min 25% 50% 75% max 上限临界 speed 替换前 5981 65.89 29.96 3.55 52.70 57.61 60.74 142.74 72.80 替换后 5981 55.10 11.57 3.55 52.70 57.61 60.74 67.4 volume 替换前 6045 63.68 39.03 0 30.00 64.00 91.00 182.15 182.5 替换后 6045 63.68 39.03 0 30.00 64.00 91.00 182.15 occupancy 替换前 6045 10.21 10.00 0 3.50 8.24 12.60 107.65 26.25 替换后 6045 9.45 7.28 0 3.50 8.24 12.60 26.17 2.阈值理论法 此外，根据交通流理论，地点平均速度v为0，流量q不为0；流量q为0，但占用率O和地点平均速度v同时不为0；占用率为0，流量大于设定值。[3]对于交通流模型，在阈值理论中，平均速度v的取值范围为0 ≤ v ≤ fv⋅v1，其中，v1为道路的限制速度，单位为km⋅h^-1，fv为修正系数，一般取1.25~1.5；流量q的取值范围为0 ≤ q≤ fc⋅C⋅T/60，其中，C为道路通行能力，单位为veh⋅h-1; T为数据采集的时间间隔,单位为min；fc为修正系数，一般取1.25~1.5；占用率O的取值范围为0≤ O ≤100%。[4]这里，根据城市道路一般限速为60 km⋅h^-1，取修正系数fv=1.25，可得速度阈值为75 km⋅h^-1；道路通行能力取1520 veh⋅h^-1，fc取1.5，T为5 min，可得q的阈值为190 veh；根据实际情况推理，若路面保持畅通，则占用率O应处于一个合理范围，此处，将O阈值取为90%。根据以上得到的速度、容量和占用率阈值，设定异常值清洗规则，得到结果如图1.4和表1.3所示。由图1.4可以发现，由实际情况通过计算出发得到的直方图和核密度曲线与由箱线图法得到的结果基本相似，这说明两种方法得到的结果相似度高，模型具有较高的准确性。 
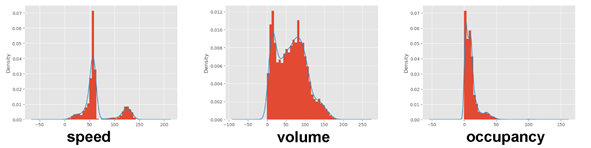图1.4 直方图和核密度曲线
表1.3 异常值处理前后的统计描述对比 count mean std min 25% 50% 75% max speed 替换前 5981 65.88 29.96 3.55 52.70 57.61 60.74 142.74 替换后 5981 56.43 13.17 3.55 52.70 57.61 60.74 74.06 volume 替换前 6045 63.68 39.03 0 30.00 64.00 91.00 182.15 替换后 6045 63.68 39.03 0 30.00 64.00 91.00 182.15 occupancy 替换前 6045 10.21 10.00 0 3.50 8.24 12.60 107.65 替换后 6045 10.30 9.85 0 3.50 8.24 12.60 86.93
5.1.3缺失值的线性插值模型的建立与求解 8
经过对原始数据的清洗，数据的准确性得到了很大的提高，在此基础上，现将对缺失数据进行填补。对于缺失数据的填补，常用的方法为插值法，包括分段线性插值和分段二次插值等方法。
5.2任务二：交通参数-时间线性拟合模型和交通参数多元回归模型 9
5.2.1求解思路 9
5.2.2数据清洗模型的建立与求解 9
5.2.3交通参数-时间线性最小二乘拟合模型的建立与求解 10
5.2.4多元回归分析模型的建立与求解 16
5.2.5数据填补 21
5.3 任务三：非平稳时间序列预测模型 22
5.3.1求解思路 22
5.3.2 ARIMA模型的建立与求解 22
六、模型评价与改进 26
七、参考文献 27
八、附录 28
import pandas as pd
a=pd.read_excel("end12.xlsx",usecols=range(1,4)) #提取第2列到第4列的数据
b=a.values #提取其中的数据
c=a.describe() #对数据进行统计描述
print(c)
import pandas as pd
a=pd.read_excel("data 1.xlsx")
print("是否存在重复观测：",any(a.duplicated())) #输出：True
a.drop_duplicates(inplace=True) #inplace=True时，直接删除a中的重复数据
f=pd.ExcelWriter('data_1.xlsx') #创建文件对象
a.to_excel(f) #把a写入新Excel文件中
f.save() #保存文件，数据才真正写入Excel文件
from pandas import read_excel
import pandas as pd
a=read_excel("data 2.xlsx")
b=a.fillna(value={'speed':a.speed.interpolate(),
'volume':a.volume.interpolate(),
'occupancy':a.occupancy.interpolate()}) #使用线性插值替换
f=pd.ExcelWriter('data22.xlsx') #创建文件对象
b.to_excel(f) #把a写入新Excel文件中
f.save() #保存文件，数据才真正写入Excel文件
from pandas import read_csv
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
a=read_csv("data 1.csv")
mu=a.occupancy.mean()
s=a.occupancy.std()
print("标准差法异常值上限检测：",any(a.occupancy>mu+2*s)) #输出：True
print("标准差法异常值下限检测：",any(a.occupancy<mu-2*s)) #输出：False
Q1=a.occupancy.quantile(0.25) #计算下四分位数
Q3=a.occupancy.quantile(0.75) #计算上四分位数
IQR=Q3-Q1
print("箱线图法异常值上限检测：",any(a.occupancy>Q3+1.5*IQR)) #输出：True
print("箱线图法异常值下限检测：",any(a.occupancy<Q1-1.5*IQR)) #输出：False
plt.style.use('ggplot') #设置绘图风格
a.occupancy.plot(kind='hist',bins=30,density=True) #绘制直方图
a.occupancy.plot(kind='kde') #绘制核密度曲线
plt.show()
print("异常值替换前的数据统计特征",a.occupancy.describe())
UB=Q3+1.5*IQR;
st=a.occupancy[a.occupancy<UB].max() #找出低于判别上限的最大值
print("判别异常值的上限临界值为:",UB)
print("用以替换异常值的数据为：",st)
a.loc[a.occupancy>UB, 'occupancy']=st #替换超过判别上限异常值
print("异常值替换后的数据统计特征",a.occupancy.describe())
f=pd.ExcelWriter('data_11.xlsx') #创建文件对象
a.to_excel(f) #把a写入新Excel文件中
f.save() #保存文件，数据才真正写入Excel文件
%%时间转换成自变量
clc
clear
close all
%%时间间隔转换
% DAY=xlsread('data 3.csv','data 3','I1:I8588');
% HOUR=xlsread('data 3.csv','data 3','J1:J8588');
% MINTURE=xlsread('data 3.csv','data 3','K1:K8588');
% k=1;
% for i=2:1:8588
% D=DAY(i,1);D_1=DAY(i-1,1);
% H=HOUR(i,1);
% M=MINTURE(i,1);
% if D~=D_1
% k=k+1;
% end
% X(1,1)=MINTURE(1,1); X(1,2)=1;
% X(i,2)=k;
% X(i,1)=60*H+M;
% end
% for i=1:1:8588
% X(i,1)=X(i,1)/5;
% end
% %曲线拟合
% 读取数据
time=xlsread('time1.xlsx','time1','A2:A5188');
speed=xlsread('time1.xlsx','time1','B2:B5188');
volume=xlsread('time1.xlsx','time1','C2:C5188');
occupancy=xlsread('time1.xlsx','time1','D2:D5188');
p=xlsread('time1.xlsx','time1','E2:E5188');
scatter3(volume,speed,occupancy,'r.');
title('流量速度占有率散点图')
xlabel('volume');
ylabel('speed');
zlabel('occupancy');
hold on
% scatter(time,volume,'r.');
% hold on
% scatter(time,occupancy,'g.');
% hold on
Cftool